Without an atmosphere we would continue to accelerate during free fall to ever increasing velocities until we impacted mother earth. Without an atmosphere our parachute would of course be worthless. Hence a soft landing on the moon requires retro rockets to decelerate to a soft landing while parachutes have been used to help decelerate the Martian landers in the thin carbon dioxide atmosphere of mars.
In the absence of atmospheric drag we would experience a linear increase in velocity with time as described by:



Where ln is the natural logarithm base e and cosh is the hyperbolic cosine function.
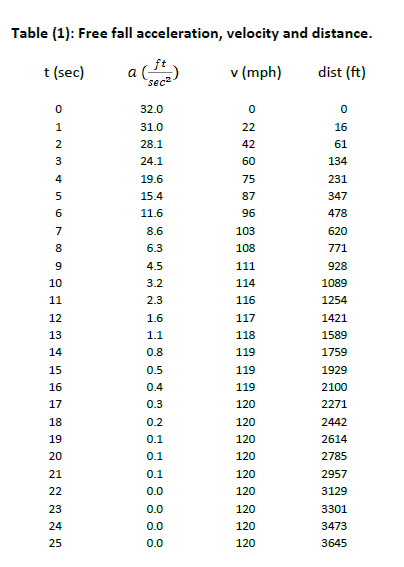
We can now evaluate eqns (10), (11) and (12) for various times over the free fall period to obtain the acceleration, downward velocity and the distance the skydiver falls. These results are tabulated in Table (1) and corresponding plots are illustrated in Figs (1) through (3).
Eqn (11) was used to calculate the plot in Fig (1). We note that as we exit the aircraft at t = 0, our initial acceleration is 32 ft/sec^2, (gravity rules). As the opposing aerodynamic drag force increases with our increasing free fall velocity, our downward acceleration decreases. We see from Fig (1) that our acceleration diminishes to about half of it’s initial value after 5 sec of free fall and all perceptible downward acceleration has ceased after 15 or 20 sec.

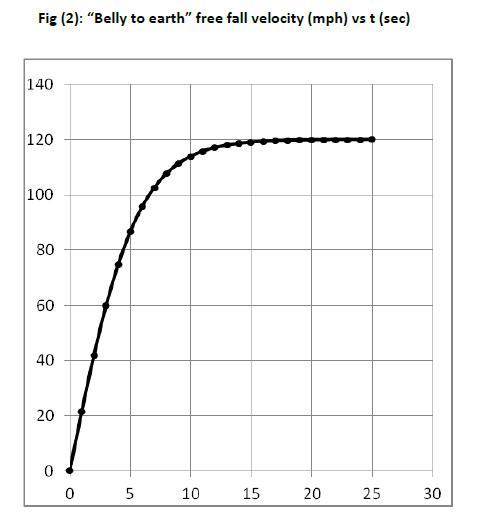
Our free fall velocity was calculated from eqn (10) and is plotted in Fig (2). It steadily increases over the first 5 seconds of free fall from zero to nearly 90 mph. During the next 5 to 10 seconds our acceleration diminishes significantly as we approach terminal. It is the post 10 sec period of the skydive when our sensation of falling is replaced by the feeling being suspended and cradled by the pressure of the wind.
Eqn (12) was use to calculate and plot the free fall distance. It is apparent from Fig (3) that we fall only about 350 feet in the first 5 seconds and at least twice that far in the second 5 seconds.
Beyond 10 seconds the plot is nearly linear as we approach a constant terminal velocity. Fig (3) confirms our often used rule of thumb “we free fall about 1000 feet in the first 10 sec and another 1000 feet for every 5 sec thereafter”. Comparing the distance at 25 sec with that at 20 sec in Table (1) we see a difference of about 860 ft, a bit less than the rule of thumb value of 1000 ft. The 1000 ft per 5 sec of free fall at terminal is only precise for a free fall rate of 1000 ft / 5 sec = 200 ft/sec or 136 mph rather than 120 mph used in this example.

Hopefully this example and discussion may provide some insight to those who are mathematically inclined and curious about the “whys”.

Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.
Note: Your post will require moderator approval before it will be visible.